AldapetaLovesDrawing: KURBA KONIKOAK

1.DEFINIZIOA ETA ELEMENTUAK KURBA KONIKOAK, KONO BAT MOZTERAKOAN SORTZEN DIREN KURBAK DIRA

Konoa nola mozten dugunaren arabera, bat edo bestea aterako da. KLIK EGIN HURRENGO LOTURAN (bertan gero, marrazkiaren gainean jarri arratoia eta kurba konikoa nola ateratzen den ikusiko duzu):

HEMEN, ikusi animazio oso interesgarria kurba konikoak ulertzeko

Ikusi dugunez, 4 plano desberdinekin konoa ebakitzean, 4 kurba koniko lortzen ditugu.

Hurrengo irudian konoaren parteak ikusiko ditugu:

Eta hauek dira 4 kurba konikoak:

1. Ardatzarekiko PERPENDIKULARRA den plano batekin, ZIRKUNFERENTZIA lortuko dugu

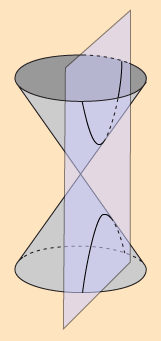
2. Ardatzarekiko PARALELOA den plano batekin, HIPERBOLA bat lortuko dugu.

3. Konoaren SORTZAILEAREKIKO PARALELOA den plano batekin, PARABOLA BAT lortuko dugu

5. Parabolaren angelua EZ DEN BESTE PLANO ZEHIAR batekin, ELIPSEA lortuko dugu.

Zirkunferentzia nahiko ezagutzen dugu, beste hiruak landuko ditugu.

2.ELIPSEA

Elipsea, konoa plano ebakitzaile zeihar batekin moztean sortzen den kurba da.

2.1.ELIPSEAREN ELEMENTUAK ETA EZAUGARRI NAGUSIAK

Elementuak, Ardatz Nagusia, Ardatz Txikia eta Fokoak dira.
Ezaugarri nagusia: Elipsearen edozein puntutik, fokoetaraino dituen distantzien batura beti berdina da, eta ardatz nagusiaren luzera (AB) balio du.

2.2. ELIPSEA MARRAZTEKO PROZEDURAK

Bi prozedura landuko ditugu: Lehenengoa fokoak aterata eta bigarrena fokoak atera gabe.
2.2.1 ELIPSEA MARRAZTEKO PROZEDURA FOKOAK ATERATA, BI ARDATZAK EZAGUTUTA
GeoGebra Hoja Dinámica

Este es un Applet de Java creado con GeoGebra desde www.geogebra.org – Java no parece estar instalado Java en el equipo. Se aconseja dirigirse a www.java.com
Amaia San Sebastian, Creado con GeoGebra

-->

2.2.2 ELIPSEA MARRAZTEKO PROZEDURA FOKOAK ATERA GABE, BI ARDATZAK EZAGUTUTA

GeoGebra Hoja Dinámica

-->

3.PARABOLA

PARABOLA, konoa SORTZAILEAREKIKO PARALELOA DEN plano ebakitzaile batekin moztean sortzen den kurba da.

3.1.PARABOLAREN ELEMENTUAK ETA EZAUGARRI NAGUSIAK

Elementuak, :
1. Ardatza: Parabola simetrikoki erdibitzen du
2. Zuzentzailea: Ardatzarekiko perpendikularra den zuzena, parabolaren kanpoaldean dago.
3. Erpina: Parabolak ardatza mozten duen puntua. Parabolaren puntua izateagatik, zuzentzailetik eta fokutik erdipuntuan dago
4. Fokua: Ardazteko puntu berezia.

Ezaugarri nagusia: Parabolaren edozein puntutik, zuzentzailera eta fokora dituen distantziak beti berdinak dira.

3.2. PARABOLA MARRAZTEKO PROZEDURAK

Bi prozedura landuko ditugu.

3.2.1 PARABOLA MARRAZTEKO PROZEDURA, FOKOA ETA ZUZENTZAILEAREN ARTEKO DISTANTZIA EZAGUTUTA

GeoGebra Hoja Dinámica

-->

3.2.2 PARABOLA MARRAZTEKO PROZEDURA, VY ARDATZA ETA Y-REN GAINEKO C PUNTUAREN ALTUERA EZAGUTUTA

GeoGebra Hoja Dinámica

-->
4.HIPERBOLA

HIPERBOLA, konoa ARDATZAREKIKO PARALELOA DEN plano ebakitzaile batekin moztean sortzen den kurba da (baita sortzailearen angelua baino txikiagoa den plano batekin ere)

4.1.HIPERBOLAREN ELEMENTUAK ETA EZAUGARRI NAGUSIA

Elementuak, :
1. Ardatza: Hiperbola simetrikoki erdibitzen du
2. Ardatz erreala: Ardatzarekiko hiperbolaren mozketa puntuen arteko zuzenkia.
3. Fokuak: Ardazteko puntu bereziak.

Ezaugarri nagusia: Hiperbolaren edozein puntutik, fokoetaraino dituen distantzien kenketa beti berdina da, eta ardatz errealaren luzera (AB) balio du. Kenketaren balioa beti bere balio absolutoan hartzen da.

4.2. HIPERBOLA MARRAZTEKO PROZEDURA, ARDATZ ERREALA EZAGUTUTA
GeoGebra Hoja Dinámica

--> -->

Páginas

KURBA KONIKOAK

2 comentarios: